A new way to use color to understand music.

Isaac Newton told one of his first biographers about how he had the initial notion for his law of universal gravitation whilst sitting under a tree and watching an apple fall.

When we talk about the genesis of ideas and ideation in general, it is difficult to know which synapses will fire, or which random interactions will lead to a breakthrough.

As you'll see below, it took Johann Pachelbel, The Beatles, Bob Dylan, and Metallica to convince me that maybe there was some merit in Isaac Newton's theory of color spectra.

And not to overpromise anything, but it may change the way you look at music forever. (Hint: It starts in the section of "Can this be helpful at all?")

Bad Ideas

When I lived in New York City, I created a comedy show with my friend Ned Ehrbar, called "Bad Pitches". The premise was simple: In order to have a truly horrible idea, you have to know how to have a truly brilliant one. We would ask people to pitch their worst ideas for television shows. I remember sitting in the audience during the first pitch of the first show, hearing the roaring laughter around me, and thinking that I probably would never have an idea as good as that again.

But more importantly, it reminded me how there can be a kernel of brilliance, even in the worst of ideas. It seemed apropos to share both of these, because as I've mentioned many times, Newton was wrong.

When Newton Was Wrong

When I was researching rainbows, I noticed that nearly every pre-16th century source listed three colors for the rainbow, (with Aristotle's notable addition of a fourth color - gold, between the first and second colors).

As I mentioned, Isaac Newton changed everything with his Optics, which was based on his experiments of refraction of light using a prism, in which he listed 7 spectra of color in a ray of light (which would later be codified as ROY G BIV). He chose 7 because of its relation to the musical tones within an octave, but admitted that it doesn't really work mathematically.

I have been quite open about how wrong I considered Newton to be, which he was.

But he was Sir Isaac Newton, and I wanted to consider for a moment that he had validity in his folly. I explored various ways to mathematically divide the spectrum of light in order to create a sampling of color which would reflect the vivid spectrum of color we encounter every day.

As I wrote in a previous newsletter, I noticed that one of my lowest results which seemed to accurately sample the vibrant spectrum of color resulted in 12 hues. I consulted with a musician friend who reminded me that even in music there are 12 tones, not 7. On a piano, these so-called "half-steps" would be called the black keys, and would be called either "sharps" or "flats".

Starting from C at 0°, which could be described as "red", I proceeded to map the twelve colors to the 12 notes. At the end of that newsletter, I wrote, "I'm in the process of exploring the relationship between complementary color palettes and musical scales."

I'm not sure I would go so far to say that Newton was correct, but without him, I would have never went down this path of experimentation. This is the result of that process, and it has completely changed how I look at both music and color.

Major Scales

Feel free to skip this part if it's too confusing, too obvious, or very wrong.

In music theory, a major scale is comprised of 8 notes in an octave from the beginning and ending in the same note.

On a piano, the single-letter notes are the 8 white keys (in a complete octave), and the others are 5 black keys, which could either be referred to as a sharp of the previous whole note, or a flat of the upcoming whole note.

C Major

It's deceptively simple to show a major scale in C.

C - D - E - F - G - A - B - C

I say "deceptively simple", because in a diatonic (12 tone) scale, because the major scale progression is whole (+2), whole (+2), half (+1), whole (+2), whole (+2), whole (+2), half (+1).

Or if we show all the notes:
(1) C
(2) C#/D♭
(3) D
(4) D#/E♭
(5) E
(6) F
(7) F#/G♭
(8) G
(9) G#/A♭
(10) A
(11) A#/B♭
(12) B
(13) C

It would be more correct to say the formula for a major scale is 1,3,5,6,8,10,12,13.

D Major

For a D Major scale, we could just add 2 to each number (3,5,7,8,10,12,14,15).

D - E - F# - G - A - B - C# - D

(3) D - (4) D#/E♭ - (5) E - (6) F - (7) F#/G♭ - (8) G - (9) G#/A♭ - (10) A - (11) A#/B♭ - (12) B - (13) C - (14) C#/D♭ - (15) D

Musicphilia meets Colorphilia

As I had written in the previous newsletter on the subject, this is an issue of sampling. It's overwhelming to choose all the millions of hues of color in a ray of light. It's even overwhelming to choose the 360 hues we would get if we were simply choosing to select one hue each 1° of the 360° spectrum.

As I had mentioned there, choosing one hue every 30° works well, resulting in 12 hues. The problem is that the green spectrum is from around 65° to 165° (around 100°), while the red + orange + yellow spectra combined are a cumulative 65°.

How do we mathematically select a smaller subset which allows us to get widest variety of hues in the lowest amount of colors? And for that, we can borrow the formula for calculating a major scale.

C Major Chromatic Scale

Using the C major scale, we would get:

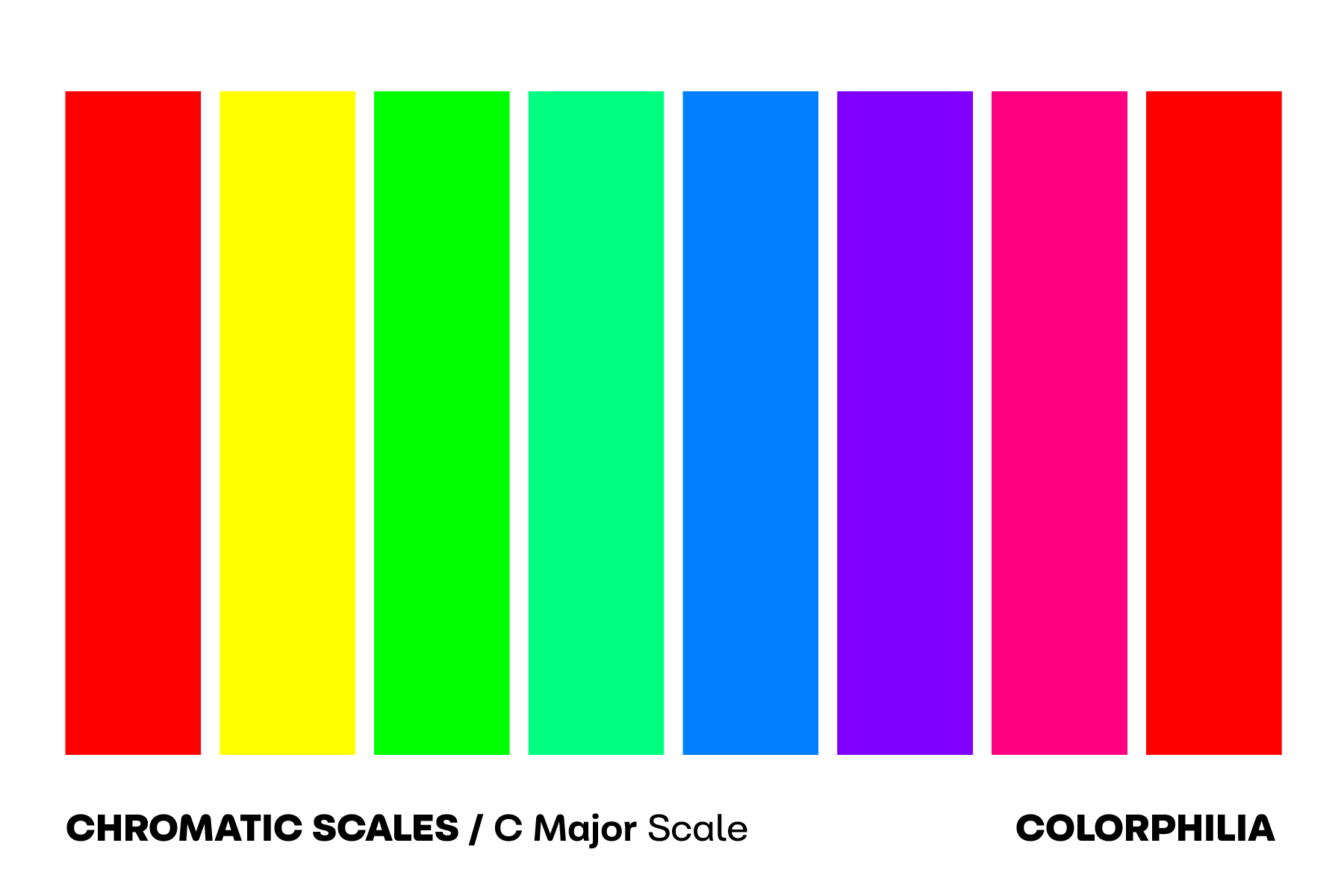
As people seem to like the color "orange", we need to choose a different starting point.

D Major Chromatic Scale

Applying the same exact algorithm, but starting at D, we find:

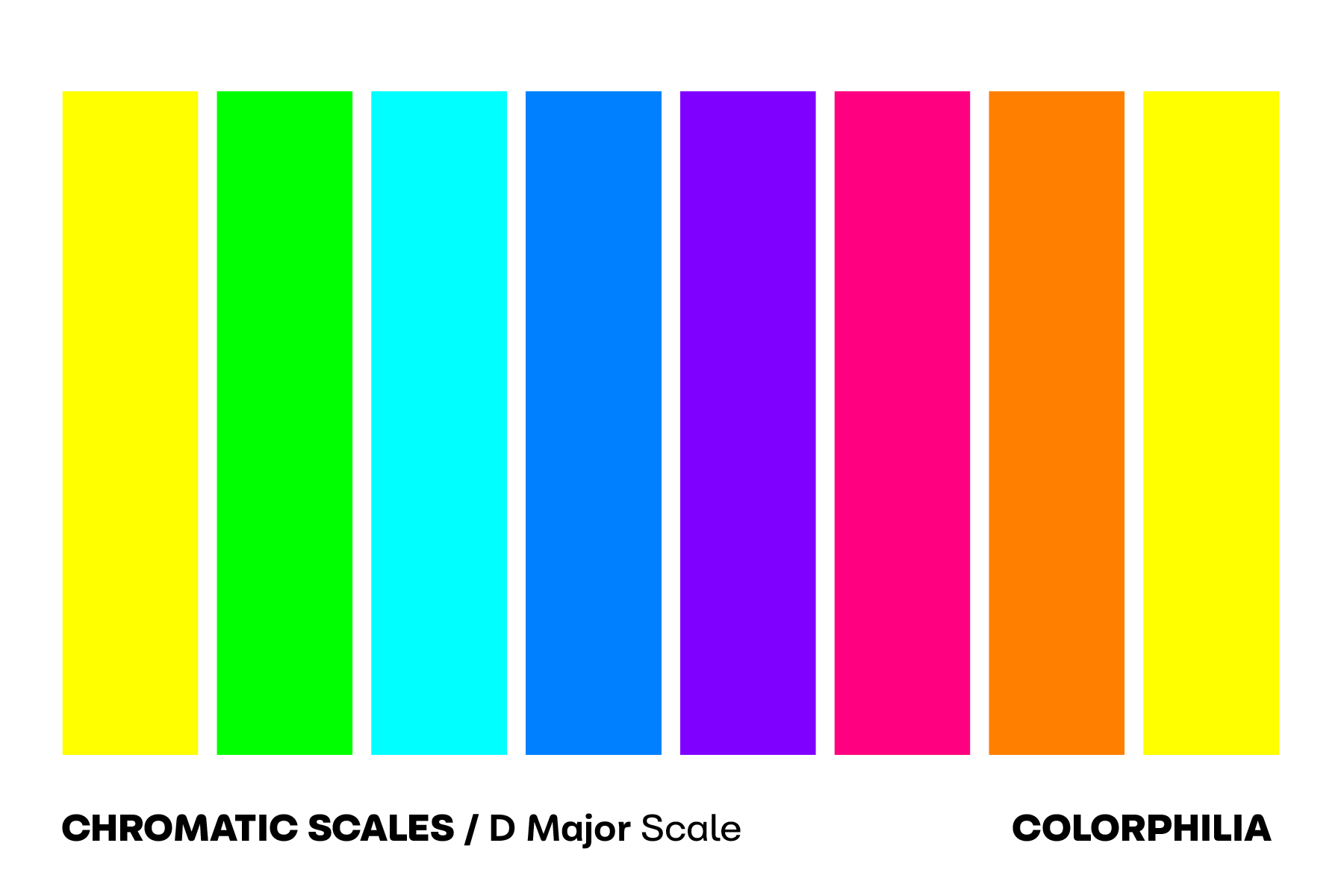
It's a pretty good selection, but it doesn't exactly have any color that can be described as "red", unless, we consider 330° (B) to be "red". Historically, 330° is closer to the color of flamingos, whose name was a hieroglyph for red in Ancient Egypt.

And this is somewhat by design: based on the construction of the formula, 0° (red), 30° (orange), and 60° (yellow) will never appear together in a major scale. You would need to have three consecutive "half-steps".

But, this starts the spectrum at yellow, which feels off.

(B) Minor Justice for Newton

The calculation of a natural minor scale is slightly different: the formula for the natural minor scale is whole (+2), half (+1), whole (+2), whole (+2), half (+1), whole (+2), whole (+2). This results in discrepancies between every major scale and natural minor scale in the 3rd, 6th, and 7th colors.

The relative minor of a major scale contains the same notes, albeit in a slightly different order. The relative minor of the D major scale is the B minor scale, which is as close I can approximate to ROY G BIV, in the proper order. To paraphrase Newton, this is mathematically accurate, but not quite good enough for practice.

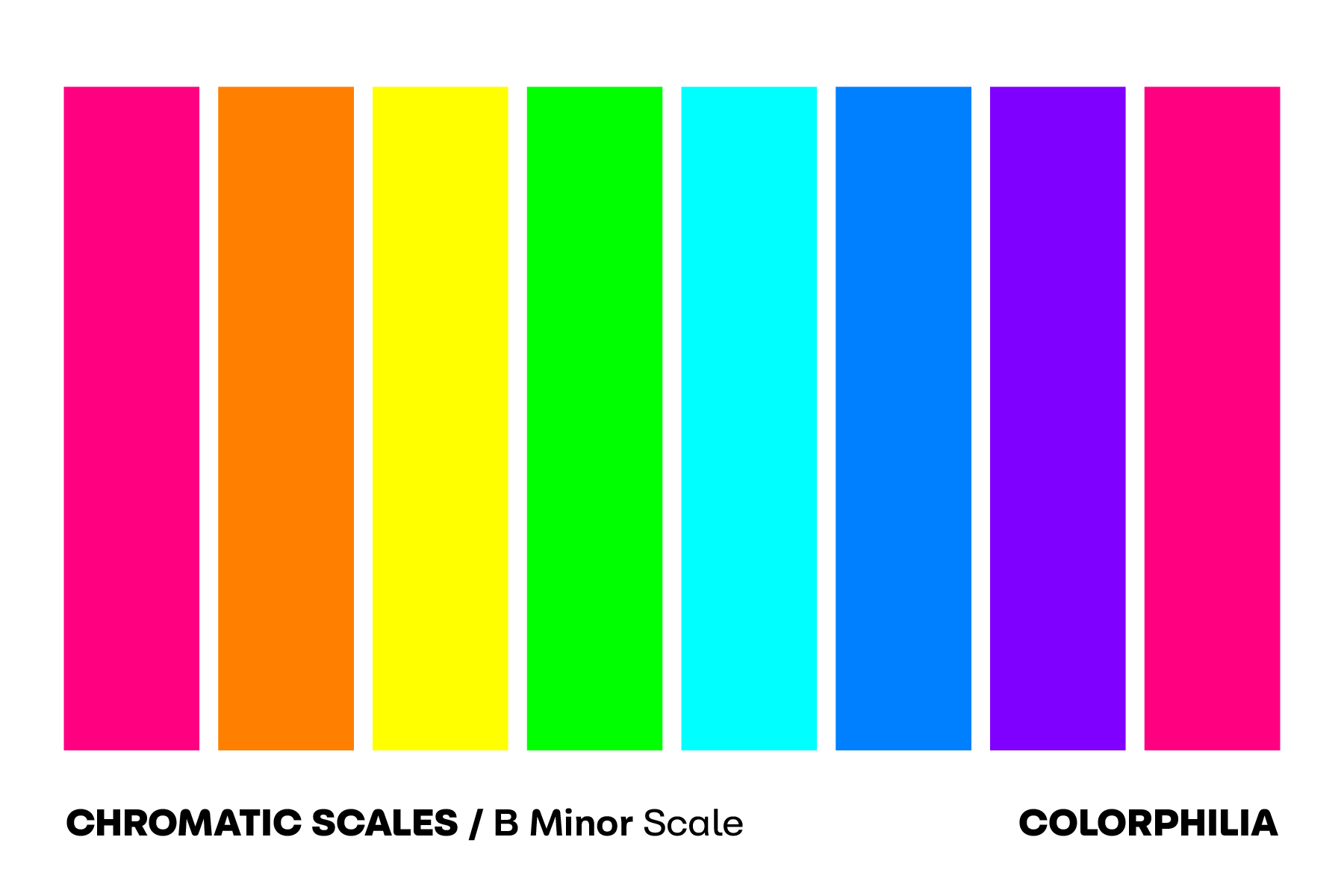
Can this be helpful at all?

If we apply these colors to notes, it can change how we learn and perceive music.

Growing up, I always heard that if you wanted to play in a rock band, all you needed to learn was how to play three chords on the guitar. I'm sure that was an exaggeration, but many popular songs are based on three chords.

Chromatic Chords

Every basic major chord (major triad) is comprised of three notes, all constructed with the same structure: the root, its major third (4 semitones x 30° = root + 120°), and its perfect fifth (7 semitones x 30° = root + 210° ).

Sounds easy enough?

Three of the first chords one learns are D major, G major, and A major.

For example, with just those, you can play:

• Bob Dylan's "Mr. Tambourine Man"
• Tom Petty's "Free Fallin'"
• Deep Blue Something's "Breakfast at Tiffany's"
• The Beatles' "Twist and Shout"

Using color, even the biggest novice can spot something with these chords.

When ordered as DGA, it seems like a rather random arrangement of color.

But ordered as DAG, we can immediately spot a pattern - the D Major chord ends with a purple A (270°), and G Major chord ends with a yellow D (60°). It makes sense why it would be easy to strum.

We can also easily count that there are a total of 7 notes used: D F# A G B C# E. Which happen to be the same notes in the D Major scale from above.

Mapping Songs

Using the same method, I wanted to see if I could better understand the structure of music as well.

Pachelbel's Canon

I had been trying to map out the Baroque composer Johann Pachelbel's famous "Canon" by chords with colors and realized that only 7 colors were used, which seems quite obvious in retrospect, as it is called "Canon in D".

Intro to "One"

In 1999, Metallica released a two-disc album of a concert they performed with the San Francisco Orchestra called S&M (Symphony & Metallica). To me, the pairing made sense, because regardless of lyrics or vocals, their music always seemed classical in nature.

I had always considered the intro to one of the songs on their album ...and Justice for All, titled "One" to be quite hauntingly beautiful. (Here is a music-only rendition performed by a pianist on YouTube.)

By their names alone, the chords didn't tell me anything.

Bm - Gmaj7 - Bm - Gmaj7 - Bm - Bm/A - Gmaj7 - E5 - F#sus4

Using this new color language, I mapped out the chords and had a few discoveries. Not only did it seem to be repeating the phrase B-D-F#, I was able to see the dark blue G (210°) as a form of punctuation, and then the purple A (270°), and the green E (120°) comes in towards the end, and the section is completed with the orange C# (30°).

Looking at these chords, B-D-F#-G-A-E-C#, I saw that the C# was the final missing note in the B minor scale, and the song would have felt incomplete without it. The final few chords also don't include the upbeat D.

As I had written above, B Minor is the relative minor of D Major, and therefore contained the same collection of notes. (It should be noted that when the song is performed live, the guitars are tuned down one semitone.)

A Hyper-versatile Palette

Johann Pachelbel, The Beatles, Bob Dylan, and Metallica, were all effectively painting using the same palette of sounds, with extremely different results. And this hyper-versatile color palette was effectively the same one Newton chose to convey the spectra of colors embedded in every ray of light.

Composers and visual artists alike can do a lot when restricted to a particular palette. The same notes or colors can make you want to celebrate a bride, twist and shout, lament the hardships of life, or commemorate the horrors of war endured by soldiers in the First World War.

Seeing Music

I spoke with scores of people at the Andersonville Arts Weekend in Chicago yesterday, organized by the Andersonville Chamber of Commerce, where I had a booth and was explaining this collection to random passerby.

As luck would have it, I was sitting next to the booth of the members of the Lakeview Orchestra who were trying to get people interested in attending their upcoming season (with ticket prices ranging from $17-50, and $14 for students/children).

It was quite validating to chat with various members of the orchestra and see their excitement mirror my own.

I'm not a musician nor do I have synesthesia, though I did chat with a brilliant musician who is, in fact, a synesthete. He told me that his favorite chord was Eb Major, so I created its chromatic scale for him. His immediate reaction was that the chord always seemed lush and green to him.

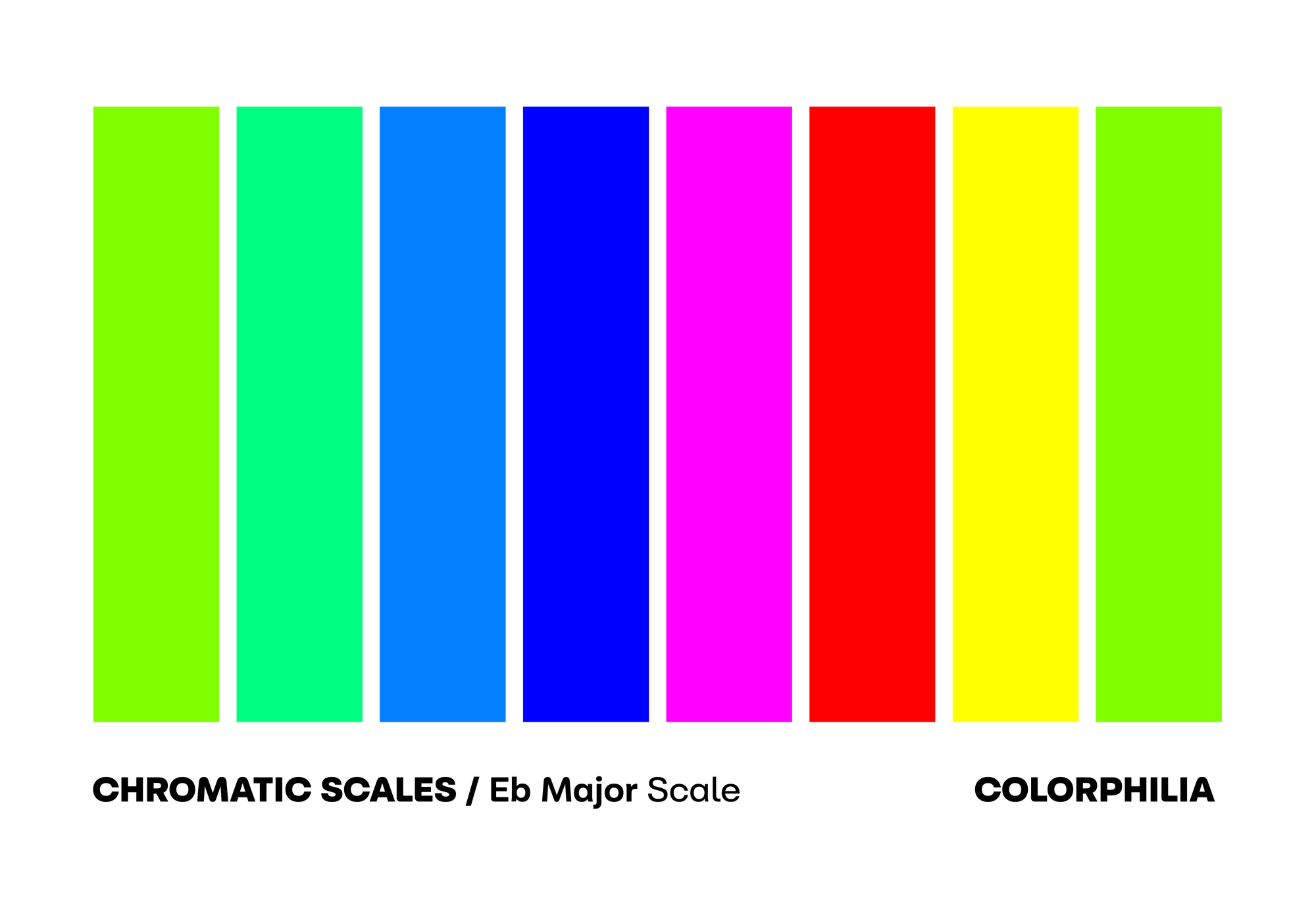
It echoed what some other musicians told me. That quite often when teaching music, teachers may ask if students can notice the difference in the notes they are hearing. I wonder how different teachers and students can use these notes, chords, and scales to teach or learn. Even for simply studying music appreciation, it makes it easier to understand the structure of the song.