Musical Scales and Color Spectra
A reexamination of Newton's connection between the music and color.

Please note: This newsletter is filled with actual color.
When I first researched rainbows, I read various versions of Sir Isaac Newton’s Optics in a very cursory manner. My goal, at the time, was to figure out how different thinkers had perceived the colors of the rainbow.
Until Newton, the nearly universal perception of rainbows was, to more or less, describe them in a series of three color words.
It was at that time I discovered that Newton had chosen the seven color set to reflect the musical chromatic scale of a single octave. It was that mathematically inaccurate calculation which led the centuries-old incorrect, confusing, and absurdist practice of teaching schoolchildren “Roy G. Biv”, or “Red Orange Yellow Green Blue Indigo Violet” as the color of the rainbow.
As a reminder, he was writing about the refraction of a ray of light using prisms,not the colors in a rainbow. The problems remain, regardless.
Please understand that even according to Newton himself:
This Rule I conceive accurate enough for practice, though not mathematically accurate.
Newton Explained
It turns out that I, like everyone else, misunderstood Newton. He was not talking color, he was talking about spectra (spectrums) of color.
He wrote:
“...describe a circle ADF and distinguish its circumference into seven parts, DE, EF, FG, GA, AB, BC, CD, proportional to the seven musical Tones or Intervals of the eight Sounds, Sol, la, fa, sol, la, mi, fa, sol, contained in an Eight, that is, proportional to the numbers: ⅑,⅒,⅒,⅑,⅒,⅒,⅑.”
- Sir Isaac Newton - Optics - Prop. VI Prob. II
I created a little rough image to better explain his theory:
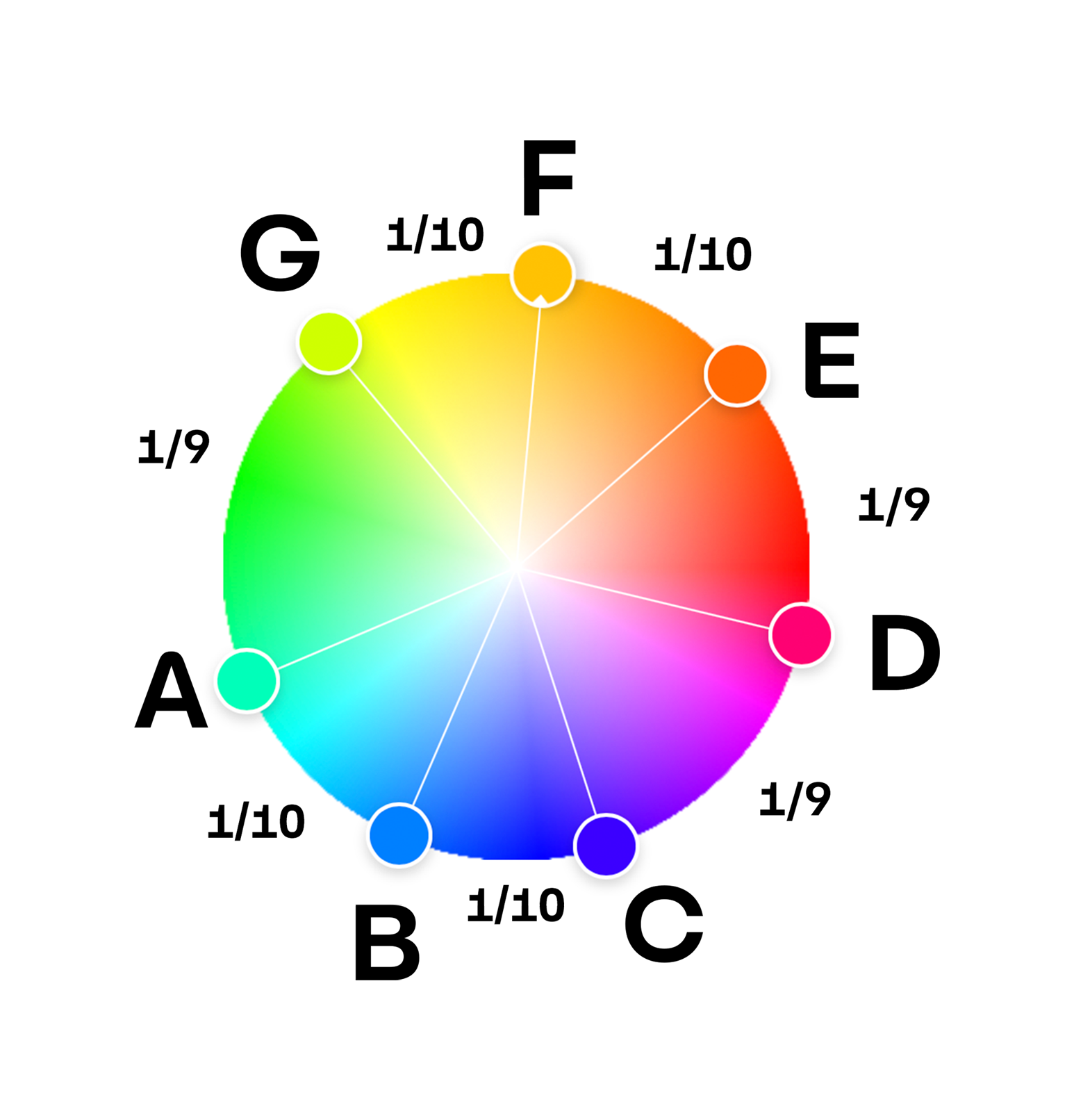
In short, instead of looking at the dots, look at the area between the letters.
- DE - Spectrum of Reds
- EF - Spectrum of Oranges
- FG - Spectrum of Yellows
- GA - Spectrum of Greens
- AB - Spectrum of Blues
- BC - Spectrum of Indigos
- CD - Spectrum of Violets
The dots themselves, in fact, are the mean (average) midpoint between two spectra of color.
- E - Mean color between Red and Orange
- F - Mean color between Orange and Yellow
- G - Mean color between Yellow and Green
- A - Mean color between Green and Blue
- B - Mean color between Blue and Indigo
- C - Mean color between Indigo and Violet
- D - Mean color between Violent and Red
The more correct way to state Newton would be "there are seven spectra of color in a ray of light refracted with a prism." I still disagree with him, for the record, for reasons I will show below.
Newton's Cheat
The reason why it doesn't exactly work is because Newton manipulated the ratios.
- CD, DE, and GA (violet, green, red) are each ⅑ (resulting in an estimated 40° each)
- EF, FG, AB, and BC (orange, yellow, blue, indigo) are each ⅒ (resulting in an estimated 36° each)
Newton's Linguistic Innovation
It turns out that Newton was purportedly the first to use the word "spectrum" in this way. Previously, spectrum (or spectre) would simply refer to a ghost, apparation, phantasm, shade, or whatever you prefer to call spirits.
As he was referring to color which was only made visible via use of a prism, I think that it is a fitting term. What is quite fascinating, and probably not a coincidence, is that spectrum (which was a ghost) became the word to describe a color's hue, while shade (which was a ghost) became the word to describe to the level of gray in a color.
Sampling
Newton was correct in connecting music and color theory. We can suppose a 360° spectrum of color or in any single musical octave. The question is how many colors or notes we need to have to best provide the most comprehesive understanding, without missing anything too important.
Having 360 distinct colors or notes would get confusing, because the difference from one to the next would be too small and instinguishable to most. But having too few colors or notes is equally as problematic.
The first problem is that you want to look for a whole number by which 360° can be divided into equal parts.
If we try to divide 360° by 7, we see an example of undersampling.

On the flip side, if we divide 360° by 36, we get a beautiful, oversampled, spectrum of color, but there are many examples where the difference between two adjacent colors is nearly indistinguishable.

Sampled Music
You can see a similar problem if you just consider the white keys in an octave on a piano, which was effectively what Newton was trying to mimic.
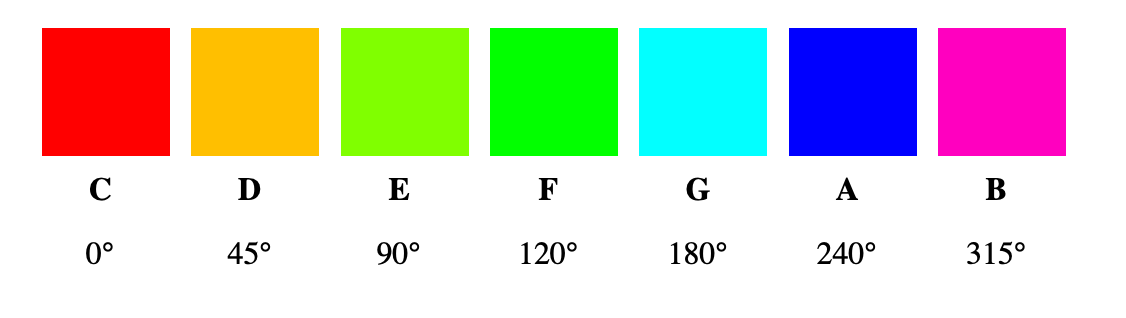
Musicians realized this limitation. It was explained to me that in a series of lectures on music theory, Leonard Bernstein explained that why the black keys were added to the piano to enable the perfect fifth, which resulted in a 12 notes in an octave.

Sampled Color
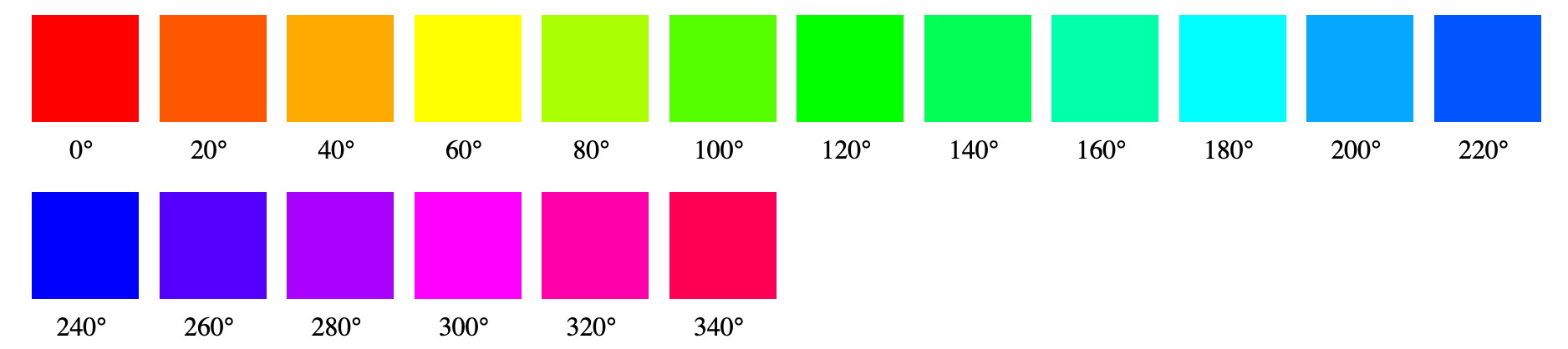
In my own experiments with the spectrum of color, I independently discovered that twelve colors (at a consistent 30°) was the number for optimal sampling. It appears almost identical to the above musical octave.

If we were to sample ten colors at 36°, we would be missing a distinct beautiful yellow.

I personally love the variety of 18 colors at 20°.
A color (or note) by any name
The problem with both color and music is that by choosing a initial sampling of 7, is that the resulting expanded samplings become referential to the first seven.
In color, this means that shades of any given color become conflated. The colors at 180° and 210° both are considered to belong to "blue", while the equally distanced 30° and 60° (orange and yellow) each receive their own respective spectrum.
In music, it means that it means that flats and sharps are manipulated and conflated in order to ensure a cohesive lettering system. In theory, C♯ and D♭are different, in practice, they are the same.
Something to consider
I'm in the process of exploring the relationship between complementary color palettes and musical scales.
For example, here is the E major scale according to the 12 notes in a musical octave:
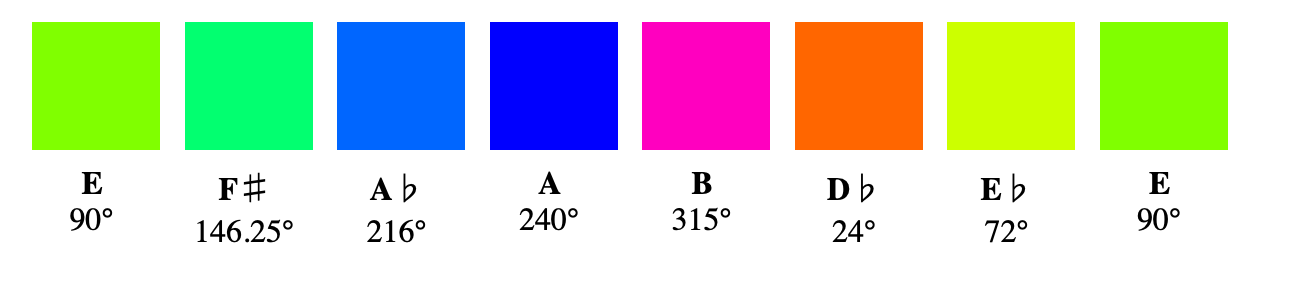
And here is the same theoretical scale based on 12 colors in a 30° color spectrum:

I know which scale I prefer visually, I just wonder how it sounds.




